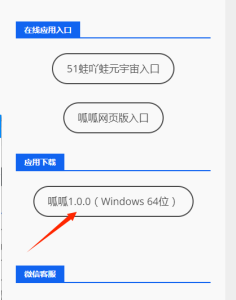
已知
,下对此结论进行证明。
欲证明
,
只需证明
,
只需证明
。
令
,易知
在
附近单调递减且有一根
。
问题转化为证明
。
注意到
,从而转化为证明
,
只需证明
,
只需证明
。
令
,
。
令
,
,从而易知在
上
单调递减,
,
,
单调递减。
从而
,都有
,
。
因而可以加强为证明
。
利用万能公式,
。
。
令
,易知
单调递减,则只需证明
,
只需证明
。
易知在
上
,则可以加强为证明
,
只需证明
。
没有了三角函数的运算变得简单得多。易知
,
,因此
。从而问题得证。
手画三角函数线或者函数图像并不能看出来;借助做图软件或者计算器就失去手算的乐趣了。有关以上两点的内容就请不要再在评论区里提及了。
捞自己一把,对运用类似的奇技淫巧证明不等式感兴趣的同学:
感谢阅读。
(2019-09-30 更新)
鉴于有同学问及,补充一下
的计算方法(其实一搜就会有很多):
几何法 1:

如图所示的等腰
中,顶角
,底角
。做
的角平分线
交对边
于
;过点
做
边上的高
,垂足为
。容易看出
,
,
,设其长为 1。由
,可得
。设
,则
,
,解得
。
,
。
几何法 2:

如图所示,两条射线成一
的角。从顶点
开始,以前一次操作得到的新交点为圆心画半径为 1 的弧并与对边相交,依次得到
;再从
、
、
、
分别向对边做垂线
、
、
、
。
各个角度已经在图中标出,其中
。从而不妨设
,
。由相似关系
可得
,再结合二倍角关系
,使用其中形式较简单的代换即可解得。一并也可得到
的值。
三角法:
设
,则
即解方程
的符合条件的根。
,解之即得。
利用
、
等诱导公式的相等关系和二倍角、三倍角公式亦可以得出结果,在此不做赘述。
复数法:
设
,
,
令
,则有
,解之即得。