分类：生活

WPeMatico Campaign中添加的类别

拉普拉斯变换中的 S 是个什么鬼？

admin 2024年8月31日

A good way of thinking of where the Laplace transform comes from, and a way which dispels some of its mystery is by thinking of power series.(一个比较好的关于 Laplace 变换的解释方法是从幂级数(Power Series)入手。)
— —Arthur Mattuck (原 MIT 数学系主任)

学过控制的都知道拉氏变换(Laplace Transform)，其可以将微分方程转化为代数方程进行运算，使得求解大为简化。

但你们是不是也有这样的疑问：拉氏变换中的

$S$

是怎么来的？皮埃尔 – 西蒙·拉普拉斯^[1]当年为啥就能想出个这样的数学变换公式？

Pierre-Simon Laplace (1749–1827)图片来源：（Wikipedia）

我是自从接触拉氏变换就一直有这样的疑问，直到有一天，看了 Arthur Mattuck ^[2]的微分方程才恍然大悟。更有意思的是，导师有一天也问了这样一个看似无厘头的问题，还好当时有所准备。

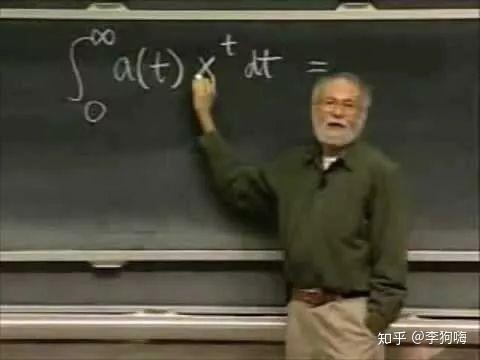
如果学过高等数学，都应该知道：一个幂级数可以写为如下形式：

$A(x)=\sum_{n=0}^{\infty}{a_n}x^n \tag{1}$

将其展开其实就是：

$A(x) = a_0+a_1x^1+a_2x^2+...+a_nx^n$

如果将其中幂级数的系数

$a_n$

看成一组离散的函数，则上式

$(1)$

也可以写为：

$A(x)=\sum_{n=0}^{\infty}{a(n)x^n} \tag{2}$

通过把

$a(n)$

看作一组关于变量

$n$

的离散函数，式

$(2)$

相当于描述了函数

$A(x)$

的构造过程。

输入是离散函数数列

$\{a_0, a_1, a_2, ⋯, a_n\}$

，输出则是由多项式构成的函数

$A(x)$

。即，只要输入一个

$\{a_0, a_1, a_2, ⋯, a_n\}$

数列，就可以输出一个函数

$A(x)$

，其中，

$x$

是输出函数

$A(x)$

的自变量。

现在，举一个例子，如果取

$a(n)=1$

，即

$\{a_0=1, a_1=1, a_2=1, ⋯, a_n=1\}$

，那么将得到输出为：

$A(x)=1+x+x^2+x^3+\cdots \tag{3}$

有人说式

$(3)$

最后等于

$\frac{1}{1-x}$

，但这么说其实不准确，因为并不是对于所有的

$x$

都成立，只有当它是一个收敛级数时才成立！

而式

$(3)$

中

$x$

的收敛域为

$x∈(-1,1)$

，所以当满足收敛条件时，式

$(3)$

可以改写为：

$A(x)=1+x+x^2+x^3+\cdots =\frac{1}{1-x},\ \ -1<x<1 \tag{4}$

再举一个例子，如果

$a(n)=\frac{1}{n!}$

，即

$\{a_0=1, a_1=\frac{1}{1!}, a_2=\frac{1}{2!}, ⋯, a_n=\frac{1}{n!}\}$

，则有：

$A(x)=1+\frac{1}{1!}x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\cdots=e^x \tag{5}$

在这个例子里，对于任意 $x$ 均成立，即收敛域为 $ℂ$ 。其实式 $(5)$ 就是函数 $e^x$ 在 $x=0$ 处的泰勒展开，或者说是函数 $e^x$ 的麦克劳林级数。

从上面的例子可以看出，取一个定义在正整数上的离散函数，然后进行无穷次的相加操作，结果却能够产生一个连续函数。而且注意其中的离散函数 $a_n$ 的变量为 $n$ ，相加得出的却是关于变量 $x$ 的连续函数。

现在，让离散求和变成连续求和，即不再是变量 $n=0, 1, 2, 3…$ ，而是另外定义一个变量 $t$ ，并且有 $0≤t<∞$ ，即 $t$ 可以为 $[0，∞)$ 中的任意数。

如果想用 $t$ 取替代 $n$ ，显然不能再用上面处理离散序列的办法进行求和，而是通过积分操作。即：

$A(x)=\int_{0}^{\infty}a(t)x^tdt \tag{6}$

式 $(6)$ 与式 $(1)$ 的区别在于：用 $t$ 取替代了 $n$ ；用积分符号替代了累加符号。

我们可以保留这种形式，但是没有数学家喜欢这样做，而且工程师也很少会这样做。因为在做微积分运算时，没有人希望其中有一个指数的底是 $x$ 之类的积分或微分项，这看起来很头疼。而唯一方便的是取指数的底数为自然常数 $e$ 。只有 $e$ 才是人们喜欢用来积分或微分，因为 $e^x$ 在微积分时可以保证自身不变函数，详见：《自然底数 e 怎么就“自然”了？》和《为什么 e^x 的导数是还是其自身？》。

因此，将以 $x$ 为底数的指数替换成以 $e$ 为底数的指数形式：

$A(x)=\int_{0}^{\infty}a(t)(e^{\ln x})^tdt \tag{7}$

既然写出这个积分当然希望其可解，或者说收敛。而只有当 $x$ 是一个小于 $1$ 的数时，即自然指数函数的幂为负数时，该积分才有可能收敛，所以这里要求 $x<1$ 。作为对数，还需要满足 $x>0$ （对数的详细介绍请见：《为什么说”对数”可以延长天文学家寿命？》），所以这里有 $0<x<1$ 。显然，当 $0<x<1$ 时， $lnx<0$ 。

$lnx$ 这个变量看起来貌似有点复杂，我们何不再用一个符号去代替它呢？

那么就用 $s$ 吧！

令 $s = -lnx$ 或 $-s = lnx$ ，因为上面说了 $lnx<0$ ，取 $-s = lnx$ 的话， $s$ 就总为正数了，处理正数当然更符合人们的习惯。另外，用 $f (x)$ 代替 $a(x)$ ，这样看上去更像我们熟悉的函数形式。这些替换只是为了修(hao)饰(kan)，现将这些替换代入式 $(7)$ 中，得：

$F(s)=\int_{0}^{\infty}f(t)e^{-st}dt \tag{8}$

通过这种方式，我们得到了Laplace Transform！

如果用符号表示这种变换，可以将式 $(8)$ 写为：

$F(s)=\mathscr{L}[f(t)] \tag{9}$

这就是 $Laplace$ 变换，当输入一个关于 $t$ 的函数，将得到一个关于 $s$ 的函数。

最后提一句，这里说的是变换，而对于一个算子来说，就不会是这样，变换和算子的最本质区别在于，经过算子运算，变量没有变，比如微分就是一种典型的算子。经过变换则会改变变量的形式，类似的例子可见：《如何给文科生解释傅里叶变换？》。

查看知乎讨论

生活

计算器的历史为什么网上都搜不到？

admin 2024年8月31日

感谢邀请。正好借这个问题，重温一下计算器的历史。这些古老的器械闪烁着旧时代巧妙的智慧，只是不幸被更方便快捷的工具淘汰掉了。

——正文分割线——

在自然科学崛起让数学变得重要，而电子计算机又尚未出现的欧洲，人们用什么计算复杂的数据呢？——那当然是一些迷人的机械计算器。

第一个重要的辅助工具出现 1617 年，苏格兰数学家约翰·纳皮尔（John Napier，1550-1617）发明了“纳皮尔的骨头”（Napier’s bones）——构造非常简单：一个方木盘左边写着行号，一大套算码的顶端写有编号，下面依次写着行号与编号的乘积。

这套工具主要用来计算乘法，计算时先用算码凑成一个因数，再根据行号读出与另一个因数每一位的乘积，格子里的斜线错位相加列在纸上，最后的总和仍要口算加法——显然，中国人根本不需要这样的工具，汉语的九九表实在太容易背诵了。

但约翰·纳皮尔的数学贡献不只是一副“骨头”，他还提出了对数概念：

若 $y=log_{a}x$ ，则 x 等于 y 个 a 连乘。

乍看上去非常复杂，但如果不考虑直接计算，就会发现对数能化幂为乘除、化乘除为加减，实在美妙。

拉普拉斯（Pierre Simon Laplace，1749-1827）因此赞叹道：“发明对数，把耗在计算上的时间减少了数天乃至数月，这倍加了，可以说，天文学家的寿命。“

然而对数表庞大得二郎神都会看花眼——而且大部分对数值不需最终保留。

牛津大学和剑桥大学很快在 1620 年到 1630 年之间发明了滑尺，将繁琐的数值改成直观的刻度，有效解决了这一问题。

仍以最简单的乘法来说：两根滑尺上的刻度是 1 到 10 的自然数的对数值，那么要计算 2×3，就只需滑动上方那根尺子，用 1 对齐 2，在右边找到 log2+log3 对应的刻度，果然是 log6。

对数尺让复杂计算变成对来对去——这就是中文“对数”一词的由来。在随后的两个世纪里，工程师和数学家不断为计算尺引入新的刻度，并添加了滑动的游标，可以计算乘除、乘方、幂次、三角函数等等复杂的计算，在 20 世纪 70 年代出现电子科学计算器以前，计算尺都是工程师的身份象征。

然而应用数学发展到这个地步，人们开始渴望一种能连加减都能免去的计算工具。

1642 年，法国数学家、物理学家和化学家帕斯卡（Blaise Pascal，1623-1662）跨出了第一步，他的“帕斯卡计算器”（Pascal’s calculator）是一个长方形的黄铜盒子，上面开了一列读数窗，下面对应着一行带辐条和指针的齿轮。先持续转动齿轮逐位输入一个加数，这将显示在上方的读数窗里；再用同样的方式输入另一个加数，读数窗里就会显示出和了。

这是第一款不需要知道计算原理的计算器，意义非同小可。

在此基础上，德国的莱布尼兹（Gottfried Wilhelm Leibniz，1646-1716）于 1672 年到 1694 年之间发明了一种“步进计算器”（Stepped Reckoner），采用了他独创的“莱布尼兹轮”（Leibniz wheel）——把刻度播到几，齿轮就转几个齿，相当于数据输入功能。除了普通的乘除法，它还能计算结果在 10 的 16 次方以内的乘除法。

步进计算器奠定了欧洲机械计算器的研发基础。在 18 世纪，各种机械计算器在欧洲雨后春笋般的涌现出来。

终于到 1820 年，法国的“四则计算器”（Arithmometer）成为第一款商业化的办公计算器，在它的带动下，一大批台式机算器进入了会计师的办公室，许多品牌一直沿用到 20 世纪。

其中，19 世纪 70 年代以后的手摇式计算器流传最广——它用齿数可变的齿轮作为输入，用跳针制成精致的进退位机构，累加器也是一套齿轮，套在滑杆上左右移动反复加减以实现乘除法；滑杆上还有一个同样的寄存器记录乘除的因数；三套齿轮互相撩拨，可以胜任 9 位数的加减乘除四则运算，对于一般的财会计算相当适用。