
可以通过其引力场来确定。
在广义相对论中,引力场被解释为质量对时空的弯曲。
一个静止的、完美球形刚体附近的时空是球对称的,而旋转的刚体附近的时空是轴对称的。
在广义相对论中,一般用“度规”来描述时空的性质。度规是时空中相邻两点之间的线元,可以看作两点之间的“距离”。
球对称时空可由史瓦西度规来描述:
其中
为质量,
为径向距离。这里使用了自然单位制,即令引力常数和光速均为 1:
。
轴对称时空可由克尔度规来描述:
其中
此时
表征中心物体的旋转。
值得一提的是,虽然史瓦西度规和克尔度规都是爱因斯坦场方程的真空解,但是根据伯克霍夫定理,只要引力源是球对称的,源外的真空引力场(度规场)就一定是静态球对称的。换句话说,用史瓦西度规来描述一个静止、完美球形刚体产生的引力场并无问题。
而利用克尔度规描述旋转的球形刚体有一定偏差,因此这里只能做一个大致估计。
如此,上述问题“如何确定一个完美球形刚体在旋转还是静止”就转变为“如何确定该刚体附近的时空是球对称还是轴对称的?”,或者说,是史瓦西时空还是克尔时空?
此时就有多种手段了,一般考虑两种情况:一种是有质量的粒子,另一种是无质量的光子。
对于有质量的粒子而言,即便拥有相同能量和角动量,它在不同时空中运动的轨迹是不同的,如下图所示
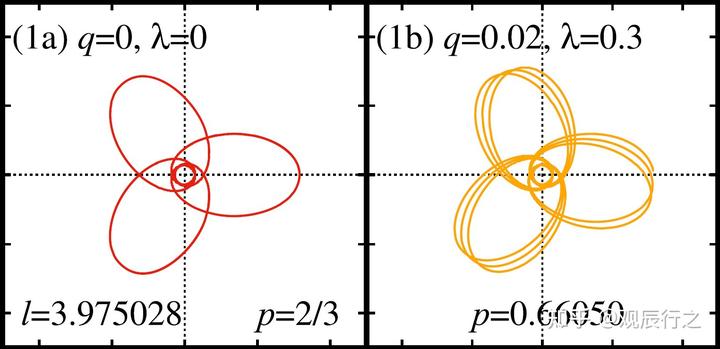
左图为粒子在史瓦西时空中运动的轨迹,右图为具有相同能量和角动量的粒子在其他时空中运动的轨迹,二者具有明显的差别。因此,可以通过粒子的轨迹来区分史瓦西时空和克尔时空。
另一方面,光子在弯曲时空中传播会发生偏折。对于不同的时空,光线偏折的角度也并不相同。
史瓦西时空中,光线偏折大致为
其中
为物体的半径。
而克尔时空中光子的偏折角与上式略有差别。因此,也可以用光线的偏折角度来区分球对称和轴对称时空。
综上,可以通过物体附近粒子的运动轨迹和光子的偏折角度来确定一个完美球形刚体是否旋转。
,,2024年8月10日,下午11:11,https://daily.zhihu.com/story/9774485

