分类： 生活

2017 年，搞笑诺贝尔物理学奖得主 M.A. Fardin 从流变学的概念出发，讨论了猫的物理状态，即物质可以根据时间表现为固体或液体，关键是观察的时间长度。

也就是通过“德博拉数（Deborah Number, De）”来衡量，这一参数最早由以色列理工学院教授马库斯·莱纳所提出，是衡量流体粘弹性的参数之一。

短时间内，猫像固体，因为它保持形状不变；长时间内，猫像液体，可以慢慢流动并适应容器的形状，比如一只猫可以“流动”进一个碗里。

科学家还观察了猫在不同表面上类似液体的行为，比如猫在粗糙表面上会“铺开”，在光滑表面上会“滑动”。总的来说，猫作为一种“主动流体”，可以自己移动和调整形状，不像普通的被动流体需要外力推动，这让它们的流动行为更加复杂。

人为什么不能自由钻行？

猫呈现液体的前提是它的身体足够柔软，但对于人类来说，头能钻过去，身子却不一定能过去（此处提醒大家不要随便钻铁栅栏）。

而对于猫来说，头能钻过去，身子就一定能过去，主要原因是人有锁骨，肩膀的宽度由锁骨的长度和位置决定，这个结构在人体中是固定的。

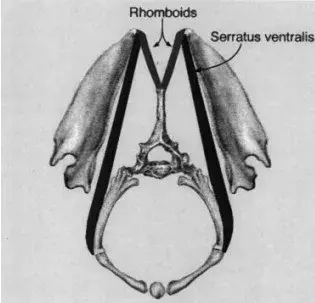
然而猫的锁骨基本退化，不像人类有明显的锁骨。因此，没有了锁骨的限制，猫可以在一定程度上压缩身体，表现出“流动性”，这也是它们能“挤”过狭小缝隙的原因。另外，猫的脊柱包含 30 块椎骨，比人类的脊柱少几块。

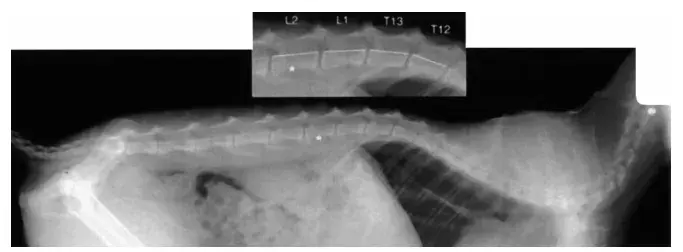
通过对猫的 X 光分析和角度测量，研究人员发现猫的脊柱在扭转方面（绕着脊柱纵轴的旋转运动）有着极高的灵活性，尤其是胸椎中段（T4 至 T11）的扭转范围非常广。实验中测量了猫脊柱在最大扭转时的角度变化，发现扭转角度接近 180 度。

而且脊柱椎骨之间的间隙较大，并且猫的椎间盘非常柔软，有助于脊柱的极大可动性。这种结构允许猫的脊柱在前后弯曲时产生更大的弧度，提供了类似“弹簧”的效果，使得它们能够快速扭转或跳跃，也能够钻过更小的空间。

除此之外，肌肉和韧带的灵活也很重要。1981 年，科学家做了一个实验，让猫尽可能地跳高，进而观察它的肌肉是如何工作的。于是发现，在跳跃等运动中，猫的后肢肌肉如半腱肌、腓肠肌和趾长伸肌等都会显示出高度协调的活动。这些肌肉在跳跃过程中通过电肌图（EMG）记录其活性，显示它们在准备阶段和发力阶段的不同反应。

该实验还测量了猫后肢在跳跃中的地面反作用力，并分析了髋、膝和踝关节的角度变化。这些数据表明，猫的关节在整个运动过程中保持极大的活动范围，从而帮助它们达到最大跳跃高度。猫的肌肉和韧带非常灵活，这有助于它们在狭小空间中调整身体姿势。

猫知道自己是“液体”吗？

在 2024 年的一个实验里，Péter Pongrácz 搭建了一个特殊的实验装置，类似于一个逐渐变窄的门框。他们召集了 30 只不同年龄、大小和品种的家养猫。

这些猫即将面对一系列逐渐变窄的开口，而科学家们则要通过观察，找出猫是否具有对自己体型的精确意识——也就是说，猫是否会提前判断自己能不能通过这个越来越小的开口，或者它们是否依赖“试一试”的方式。

然而，实验并非一帆风顺，猫在实验里是出了名的“难搞”。在一次实验里，Pongrácz 发现猫逃进了通风管道里。想象一下，科学家们准备好了一切，精心设计了一个狭窄的开口，猫的主人站在另一边，用它最喜欢的小零食吸引它，但猫却无动于衷，反而开始舔自己的爪子，像在嘲笑这些“愚蠢的”人类。毕竟，猫参与实验的唯一规则是——除非它们自己想！

起初，开口足够宽，几乎所有的猫都能轻松通过。然而，当开口逐渐变窄时，一些猫开始停下脚步，它们仔细观察狭窄的通道，有些选择了尝试，有些则转头寻找其他路线。

科学家们注意到，猫在面对狭窄但高度足够的开口时，并不会立即做出判断，而是靠近开口进行“试探”。它们的鼻子和胡须轻轻触碰开口的边缘，似乎在评估能否通过。研究人员观察到，在宽度为 12 厘米时，约有 70%的猫选择尝试通过，但在宽度缩减到 7 厘米时，这个比例迅速下降到 15%。显然，开口的宽度在 10 厘米以下时，猫会变得更加谨慎，随着实验进行，开口的高度也逐渐降低。

当它们认为自己有可能通过时，会大胆前进，身体微微压缩，灵活地钻过开口。然而，当开口变得过于狭窄时，体型较大的猫更倾向于停下来，放弃尝试。这时，猫开始显现出对自身体型的意识。

令人惊讶的是，猫在面对高度不足 15 厘米的开口时，表现出更多的犹豫。科学家们记录了它们的行为：在开口高于 20 厘米时，几乎所有的猫都会继续尝试通过，但当高度降低到 15 厘米时，超过 80%的猫停下了脚步，表现出显著的犹豫，部分猫甚至选择绕过障碍，或者放弃尝试，等待进一步的指示。

在观察过程中，科学家们还发现了一些个体差异：较年轻的猫和体型较小的猫在通过狭窄开口时显得更加大胆，而年龄较大或体型较大的猫则表现得更为谨慎。

从体重数据平均来看，体重超过 5 千克的猫在面对宽度小于 9 厘米的开口时，更容易选择放弃尝试；而那些体重低于 4 千克的猫，即便开口缩小到 6 厘米，也有超过一半的猫会选择尝试通过。换言之，在一些情况下，猫真把自己当“液体”，可以随意通过任何口子。

简单来说，如果说猫是一种“液体”，那它们也只有一个维度，是一种限高不限宽的液体。

面对同样的问题，狗的处理方式却完全不同。几年前，Pongrácz 招募了一些狗参与同样的实验。研究显示，狗在遇到不适合通过的小开口时，会减速并犹豫是否通过，有时会选择绕道。狗表现出明显的身体意识，会根据开口大小，在接近开口时做出决定。

这种对比说明了两种动物在体型意识上的差异，狗倾向于依赖更强的体型认知，特别是在面对狭小的环境时；而猫则更多依靠灵活性和试探策略来应对狭窄的空间。按 Pongrácz 的话来说，“猫可能是液体，但它们也知道什么时候停止流动。”

参考文献

[1]Pongrácz P. Cats are (almost) liquid!—Cats selectively rely on body size awareness when negotiating short openings[J]. iScience, 2024.

[2]Zajac F E, Zomlefer M R, Levine W S. Hindlimb muscular activity, kinetics and kinematics of cats jumping to their maximum achievable heights[J]. Journal of Experimental Biology, 1981, 91(1): 73-86.

[3]Fardin M A. On the rheology of cats[J]. Rheology Bulletin, 2014, 83(2): 16-17.

[4]Macpherson J M, Ye Y. The cat vertebral column: stance configuration and range of motion[J]. Experimental brain research, 1998, 119: 324-332.

策划制作

出品丨科普中国

作者丨苏澄宇

看起来，人现在就很耐受电子屏幕。随着时间流逝，广义自然选择大概会让人更擅长与电子屏幕互动。

提问者可能从网络上的糟糕来源获取了关于电子屏幕——尤其是“蓝光”——对人眼这样那样有害的垃圾信息。

这问题下还有一个回答展示了对演化的经典误解之俺寻思选择压必须是你死我活的——实际上，通过对捕食、自卫、求偶、生活质量等造成影响来出现百分之几的可育后代数量差异，就可以迅速涂改等位基因频率。

将电子屏幕与近视联系起来的说法并无真正有用的证据。人的近视更多地受遗传和每日接受较强光照（例如室外太阳光照射）的时间影响，在室内使用电子屏幕可能通过减少室外活动产生间接影响。

2024 年 6 月，我国研究人员发表的一篇荟萃分析搞了 19 项研究，结果是，使用计算机、看电视的时间与儿童近视发病率在统计上相关，使用智能手机的时间与儿童近视发病率在统计上不相关。这些相关性在东亚人群中相对显著，在欧美人群中不显著^[1]。看起来，儿童的其他行为（包括而不限于学习、户外活动）和遗传才是主要因素。

• 参考 1 提到，Swiatczak 和 Schaeffel 在 2022 年提出，智能手机的文字大小最大限度地减少了为阅读与近视建立关联的中心环绕效应 /center-surround effects，智能手机不太可能引起近视^[2]。
• 参考 1 提到，其他学者发表的类似文章频繁获得屏幕使用时间与近视无统计关联的结果。在电子屏幕于东亚普及前，近视在东亚的流行已经根深蒂固，看起来传统阅读难辞其咎。全球范围内，教育机构试图将屏幕时间与学习分开，大概是为了绕过更难解决的问题：看书、做家庭作业、书写等经常是对近视防控无正面贡献的室内近距离工作。
• 参考 1 提到，简单地限制屏幕时间可能对预防儿童和青少年近视几乎没有影响。在白天积极促进户外活动可能有助于延缓儿童和青少年的近视发作、减缓近视进展——Rose 等在 2008 年提出，这可能涉及在足够强的光照下人体分泌的多巴胺会抑制眼轴延长^[3]。参考 3 的预测已经在动物实验中得到令人信服的确认。

2024 年 8 月，我国若干研究人员发表了一篇考察使用屏幕暴露时间与老年人视网膜年龄的文章^[4]。参与者为 566 名 45 到 62 岁健康成年人，入组年龄 45 到 62 岁，考察自我报告的屏幕暴露时间、入睡时间和基于彩色眼底图像的深度学习算出的视网膜生物年龄。

结果：

参与者的平均每日总屏幕暴露时间为 4.55±2.16 小时，其中白天或开灯条件下暴露于屏幕的时间为 4.46±2.11 小时，在黑暗中暴露于屏幕的时间为 0.09±0.3 小时——作者没有解释在黑暗中暴露于屏幕的时间为负代表什么。不管怎么样，熟悉一些中老年人每天晚上是怎么玩手机的读者大概已经笑了。

屏幕暴露时间最长三等分组（每天屏幕暴露 7.07±1.6 小时）的视网膜年龄比实际年龄大 5.13±4.96 岁，中间一组（每天屏幕暴露 4.47±0.49 小时）大 2.79±4.56 岁，最短三等分组（每天屏幕暴露 2.28±0.79 小时）大 0.49±3.51 岁（负值表示更年轻）。作者似乎没有注意到三组的实际年龄分布呈现明显的递减关系。

读者觉得这种数值范围真的能用来揭示什么重要的规律吗？

• 每天屏幕暴露四五个小时的一些人的视网膜生物年龄比实际年龄小至多 1.77 岁，每天屏幕暴露一两小时的一些人的视网膜生物年龄比实际年龄大至多 4.00 岁，看起来个体差异或其他因素的影响压倒性地超过屏幕时间。
• 至于屏幕时间最长的一组，他们的实际年龄是最小的，这可能只意味着所谓视网膜生物年龄容易高估。

然后，作者粗糙地按视网膜年龄比实际年龄大的程度将参与者分成两组，声称差得较多的参与者的屏幕暴露时间通常更长。作者似乎还是完全没注意到这两组的实际年龄有重大的差异——屏幕暴露时间短、差距小的一组的年龄范围明显老于另一组。

• 两组的统计差异恐怕更多地来自生理年龄差异和视网膜生物年龄高估。

无论如何，作者声称，他们鼓捣出的线性模型显示，每日屏幕暴露时间增加 1 小时对应视网膜加快老化约 0.087 年——约 32 天。该效应在 60 岁以上人群中不显著。

• 读者可以预期，他们用来算视网膜生物年龄的程序的误差都不止这么大。
• 读者还可以仔细看看这数据与线性拟合得怎么样：

• 从数据看，作者找的几百个参与者里不乏适合每天看屏幕八小时以上的天命老爷爷、天命老奶奶。每一条曲线右侧都应该往下弯。
• 从数据看，每天屏幕暴露不到四小时视网膜还加速老化的参与者真是亏大了。如果他们怕用手机会进一步加速视网膜老化，那么建议他们用手机听广播吧。
• 更务实的建议是，不用担心这个。这文章仍有可取之处：作者指出，在黑暗中玩手机对视网膜年龄的影响看起来全部归因于入睡时间拖延。
• 这让各种渲染关灯玩手机这样那样有害的糟糕来源情何以堪。
• 可惜，作者在尝试解释有其他光源时玩手机造成的影响为什么占比下降时再次俗套地大谈活性氧什么的。
• 如果手机屏幕的光（无论是蓝光还是什么光）能通过活性氧造成可测影响，那么在黑暗中玩手机为什么完全没有表现出这种影响？
• 作者该不会以为中老年人在黑暗中玩手机时都将手机屏幕亮度调到了最低吧？

兰道尔·门罗教育我们说：

也可以想到我回答过的这个：

女子长期侧躺玩手机致右眼短暂失明，双眼眼底产生豹纹状病变，如何从医学角度解读？如何科学用眼？

关于蓝光：

“蓝光危害”是日光性视网膜炎和眼科仪器医源性视网膜损伤的主要原因或至少主要原因之一。这被某些商家有意曲解为“显示器蓝光伤眼”。

• 持续暴露于大量蓝光可通过光化学机制损害视网膜细胞，以线粒体衍生的活性氧等介导蓝光诱导的视网膜色素上皮细胞死亡^{[5] [6] [7]}；
• 蓝光可通过类似机制诱发氧化损伤、引起 Müller 细胞凋亡，但是源自 Müller 细胞、自我修复能力增强的不死化细胞系 MIO-M1 对同等强度的蓝光几乎无动于衷^[8]。

整体上，跟超重、睡眠不足、高血压等现代常见健康问题相比，来自智能手机·平板电脑·液晶电视·笔记本电脑等家用电子设备的蓝光的量引发黄斑变性、失明或眼睛其他部位的损伤的概率可以忽略。随机对照试验不支持普通人群使用“防蓝光眼镜”之类改善视觉表现或睡眠质量、减轻眼睛疲劳或保护黄斑^[9]。你可以自行寻找更多这类研究，例如参考这篇综述^[10]。

或许一些人因遗传因素而对显示器散发的蓝光比常人更敏感。那也不一定统计显著。

• 一项针对 3905 名没有近视家族史的波兰学生的统计显示，在两岁前一直开着室内灯睡觉与学龄期是否出现近视无关^[11]。这项研究未发现夜灯选择白炽灯或荧光灯对近视患病率的影响，尽管二者的蓝光光子量差异十分大。
• 一项类似的研究考察了 3636 名学生，发现开荧光灯睡觉与远视发生率增加在统计上相关，白炽灯与远视在统计上无关，开灯睡觉与屈光不正患病率在统计上无关^[12]。
• 一些双相情感障碍患者的睡眠障碍和昼夜节律可能受防蓝光眼镜等影响，但是睡眠质量和情绪控制的变化在统计上不显著^[13]。

一些广告商已经因吹嘘防蓝光眼镜等产品的功效而被罚款^[14]。

对白天在户外活动的人来说，阳光是蓝光的主要来源。一定量的白昼户外活动在统计上关系到儿童近视发病率明显下降^[15][16]。一般认为这是因为人眼的正常发育与功能维持需要足够强的光照，足量蓝光参与减缓眼轴生长、防止近视发生与发展。亦有研究显示强光与弱光都和近视发生率降低有统计关联^[17]。

• 全球范围内，统计显示，近距离工作的时间较多、户外活动的时间较少、教育水平较高、父母有近视史与患近视的风险上升相关^[18]。
• 在白天接受足量蓝光照射可参与促进或维持人的警觉性、记忆力、认知能力^{[19] [20] [21]}。
• 老年人做手术后睡眠质量改善，部分原因是人造晶状体跟老年人自带的比起来更不黄、允许更多蓝光抵达视网膜^[22]。
• 大型流行病学研究显示，防蓝光人工晶状体不会降低年龄相关的黄斑变性的发病率，也不会减慢病情发展速度。蓝光滤镜不能减少失能眩光的影响。蓝光对在昏暗的环境中避免老年人摔倒很重要^[23]。

人在注意力集中于显示器时眨眼频率下降，可以引起润滑不足、造成眼睛不适。人在夜间被大量蓝光射入眼睛可能影响褪黑素分泌，进而影响睡眠或昼夜节律。睡眠不足至少能引起一部分人的皮质类固醇水平上升、雄激素水平下降，降低眼泪分泌量和闭眼时长、影响眼泪脂质含量，或许会间接地影响眼睛^[24]。将屏幕调得更黄之类在这方面的保护作用其实也存疑。

一项针对 5865 名 6 到 18 岁学生（平均年龄 11.9 岁）的统计显示，每天阅读和写作（主要是写作业）超过 2 小时 、每天使用计算机超过 0.8 小时的学生近视发生率更高。没有发现每天看电视时间超过 2 小时的学生的近视患病率增加^[25]。似乎看电视时的用眼距离较远、房间光照整体情况较好、注意力不那么集中。

来简单举几个栗子。

正如其他答主所言，古籍从影印本的繁体竖排到可供大众阅读的简体横排的过程中，信息的准确度是在不断降低的。其中讹误的出现可能是由于影印技术的不完善，也可能是由点校者的一些“人为失误”造成。前者当然无法避免，而后者我们应当努力减少。

比如说，清朝有个诗人叫黄景仁，他写的一组《感旧》诗非常有名，一共四首，在这里只摘出其四：

从此音尘各悄然，春山如黛草如烟。泪添吴苑三更雨，恨惹邮亭一夜眠。
讵有青鸟缄别句，聊将锦瑟记流年。他时脱便微之过，百转千回只自怜。

如果有了解过一些格律，应该很容易看出：全诗作为七律只有鸟字出律，鸟那个地方应当是一个平声字。进而可以猜想，这里出现讹误的可能性很大。

http://ctext.org/library.pl?if=gb&res=4148&remap=gb在“中国哲学书电子化计划”里面搜《两当轩集》的影印本，这个字找出来是长这样的：

（鸟 —->鳥 乌 —->烏）。。。这能看出来个鬼啊(/#-_-)/︵┻━┻

作为对比，只好分别再找出这个文档里的“鸟”字和“乌”字（左边是“讵有鸟雀来空庭”，右边是“至者乌可知”）

和前面一对比，便可推断此处应是“乌”字无疑。

顺便拍了张手头一本上古出版的《两当轩集》，里面同样错印为“青鸟”：

第二个栗子就不那么费眼了，是一个朋友发在群里的，容我无耻地盗过来。阮大铖的《咏怀堂诗集》：

读下来发现后半段，尤其“寸寸皮尔曹”压根不是人话，韵也压得乱七八糟。正确的点法应该是这样：

扬州十万户，掘土为朝餐，太守闻之伤心肝。寸寸土，寸寸皮，尔曹乏食攘我为？

平水韵里面餐、肝同属十四寒，皮、为都在四支。改过之后，这几句就读着舒服多了。

所以哪怕是看起来不那么友好的点校过的“繁体字竖排”版本，相较于影印版也可能已经有些舛误了。在这个基础上出版简体横排，一些小错误只会越积越多（比如丧心病狂的“讵有青马缄别句”，网上一搜一大把……）

这些错误能被找出来，原因仅仅是我作为读者，碰巧懂一点平仄，大概分辨得出来啥和啥押韵。假如读者某一方面的知识储备不足，也许书中的某些舛误就会随着读者一代一代传下去。开个脑洞，有没有可能因为保存手段不够好、抑或是受点校者和读者知识所限，我们读的某些冷门书籍，相较于最初的版本早已经“面目全非”了呢？

出版物越接近古籍原本，可能产生的舛误就越少，我们在阅读时获得的信息也就越精确。也许“青乌”换成“青鸟”“青马”不影响表达，一首诗断成“寸寸皮尔曹”也能凭脑补凑出大意，但某些书籍——比如据说长沙马王堆汉墓挖出的《道德经》帛书本，就与当下市面流行的版本多有出入。《道德经》一共只五千个字。如果报道属实，一点微小的纠正都有可能意味着，与之相关的整个知识体系的重建。

当然，不是鼓励每个人都去读影印本，这不现实也并没有必要。作为读者，在能力范围允许内，尽量保持一个严谨的态度和一点对知识的尊重就足够了。同样，这个回答也可能会有不妥当之处，希望及时指出。

最后偏个题，放上吴王的一篇文章，尬膜。学诗与治学

 

弗里西亚马（Friesian horse）。你很可能认为它是一座金属的雕塑，然而它真的是活生生的马，中世纪欧洲的战马。这匹马名叫弗雷德里克大帝（Frederik The Great），被评为世界上最帅的马。

 

西马尼乌鸡（Ayam Cemani）。真正的铁公鸡不是？其实就是乌骨鸡，产于印度尼西亚。由于基因变异导致纤维色素增生，这种现代鸡全身漆黑，连骨头和内脏都是黑的，只有血液保持正常颜色。

 

角蜥（Phrynosoma）。身上的尖刺虽然看起来不太像金属，然而质感十足，可以吓跑敌人。实在吓不跑的时候，它会从眼睛里喷出鲜血，最远可达两米，由于血液腥味十足，吓不跑敌人，也会令它们掩鼻而退。

 

棕树凤头鹦鹉（Probosciger aterrimus）。生活在印度尼西亚、新几内亚及澳大利亚，感觉像是凶猛的绅士。

 

鳄龟。古典的青铜战士，事实上鳄龟是地球上现存最古老的爬行动物，体型大，可达近百公斤，具有强烈的攻击性。

 

鳞角腹足蜗牛。如果说前面的动物还只是看起来像重金属，那么下面这两种就是货真价实的金属装备了。这种蜗牛的外壳虽然不是金属单质，但它是由硫化铁构成，腹足则是矿化铁构成的鳞甲，真正的金属光泽。

 

血虫（bloodworm）。一种多毛纲吻沙蚕科的蠕虫，一对钳口也是货真价实的金属光泽，一种有毒的氯铜矿（Atacamite），在自由女神像及古代青铜文物上也有发现。

2018 年，89 岁高龄的菲尔兹奖得主，迈克尔·阿蒂亚爵士举行了他最后一次公开的数学报告：

这个报告是关于“黎曼猜想”的证明，报告结束后仅仅三个月，老爷子就溘然长逝。

这次报告到底是不是证明了“黎曼猜想”，我没有资格评论，这需要数学界内部进行审查。哪怕就算结果错的，也有可能指出新的突破方向，这在数学史上也层出不穷。留待学界、时间来检验吧。

但是，黎曼猜想：

函数的所有非平凡零点的实部都是 。

到底说了什么，能让这位耄耋老人在生命的最后一刻依然向它发起冲锋；让一代代的数学家为之魂系梦绕（大数学家希尔伯特就说过，如果他能复活，第一件事情就是要问问，黎曼猜想证明了吗？）。

逝者安息，生者传承，下面就以我们的方式尽量数普一下黎曼猜想，把老爷子这份执着传递一二，把无数数学家的这份执着传递一二。

1 素数

大于 1 的自然数中，除了 1 和该数自身外，无法被其他自然数整除的数称为 素数（Prime Number），比如

。

我们知道素数是无穷的（欧几里得定理），也可以通过埃拉托斯特尼筛法筛出有限个的素数：

但对于素数的整体了解依然非常少，素数似乎是完全随机地掺杂在自然数当中的一样，下面是 1000 以内的素数表，看上去也没有什么规律（你说它越来越稀疏吧，

又突然连着出现

个素数，和

以内的素数个数一样多）：

别说素数的精确分布了，就是随机抽取一个足够大的自然数出来，要检验它是否是素数都需要经过一番艰苦的计算。

以研究素数为核心的数论，在数学家眼中就是：

数学是科学的皇后，数论是数学的皇后。—- 高斯

你可能会有一个疑问，研究素数干嘛？可以改善生活吗？提高寿命吗？粮食增产吗？移民火星吗？

当然可以给出一些现实的理由，比如流行的区块链中的加密算法就依赖于素数分布的一些理论。但是随着了解的深入，我发现对于数学家而言这些根本不重要，不足以构成驱使他们前进的动力。正如有人询问著名登山家乔治·马洛里“为什么要登山”，马洛里回答道：“因为山在那里”：

数学家研究素数的理由很简单，因为它在那里。数论可能才是最纯粹的数学，才是数学的初心。

2 素数计数函数

先根据之前给出的素数表绘制一个函数图像：

纵坐标

表示的是

以内素数的个数。比如从图像上可以看出：

这个意思就是

以内有

个素数（我们知道分别是，

）。这个

被称为 素数计数函数（Prime-counting function）。

得到素数的精确分布目前还属于天方夜谭，数学家就退而求其次，想知道

到底是多少？这就是几千年来素数研究的核心问题。

3 素数定理

高斯和勒让德猜测：

后来又有改进的猜测：

把这三个函数图像放在一起，看上去好像确实可以看作近似，并且后者近似还要好一些：

这两个猜测，尤其是后者，都可以称为 素数定理（The Prime Theory），只是此时还没有证明。

4 《论小于一个给定值的素数的个数》

格奥尔格·弗雷德里希·波恩哈德·黎曼（1826－1866）德国数学家，黎曼几何学创始人，复变函数论创始人之一：

1859 年黎曼被任命为柏林科学院的通讯院士，作为见面礼，黎曼提交了他唯一关于数论的论文，也是唯一完全不包含几何概念的论文，《论小于一个给定值的素数的个数》：

这篇论文总共只有9 页，却可以名列最难读的论文之列（黎曼显然高估了阅读者的水平，其中不少结论都没有给出证明，因为他觉得不证自明、一目了然。但是事实是，比如其中证明的一小步，都花费了后人 46 年的时间才证明出来），同时又是素数研究领域最重要的一篇论文。

听这个论文的名字也知道这篇论文是关于

的，确实，在这篇文章中，黎曼居然给出了素数计数函数的准确表达式：

先不管这个函数的细节，看到没，黎曼压根就没有理会什么素数定理，直接给出了

的精确表达式，这就是王霸之气，不玩擦边球，来就直捣黄龙，解决主帅。

5 黎曼猜想

的表达式并不简单。想想也可以理解，要是初等数学就可以解决的问题，很可能早就被欧拉、高斯这两位数学守门员（形容不要想在这两位大神手里捡漏）给征服了。

重复一下，

长这样：

这个函数分为两部分：

• 黎曼素数计数函数：就是式子中的 ，下面是它的代数表达式：
  实际上是黎曼给出的对 的近似，也称作 黎曼素数计数函数 ，这个代数表达式的含义之后会细说
• 修正项：也就是：
  其中 称为莫比乌斯函数，具体的代数表达式如下：
  

整个式子的意思就是，通过修正项调整之后，黎曼给出的素数计数函数

就完全等于

了。

5.1

函数与非平凡零点

要把

介绍清楚，先得引入一个

函数 ：

为什么自变量用

，不用

呢？因为这是定义在复数域上的函数，即

，而复数域习惯用

来表示自变量（之前我就介绍过了，实数的问题如果解决不了，可以尝试升维到复数中去）。

如果尝试解下面与

函数相关的方程：

这个方程的解有无数多个，可以分为两类：

• 平凡解： ，也就是所有负偶数。这个解看上去就比较简单，也很容易求，所以叫做平凡解，也叫做 函数的平凡零点
• 非平凡解： ，也就是复数解。这类解就很复杂，现在都没有求出所有的解，而且估计求出这所有解的难度不亚于求出素数的精确分布，目前只是通过暴力运算求出了一些。所以叫做非平凡解，也叫做 函数的 非平凡零点

至此，黎曼猜想中最重要的两个名词都出现了：

函数、非平凡零点。

5.2 黎曼素数计数函数

好，回头再来看

：

这个函数有 4 部分：

• ：这个是之前提到过的，关于 的一个近似
• ： 就是指的 函数的非平凡零点，就是说把所有非平凡零点的 加起来
• ：这是一个常数
• ： 越大，这项越趋近于 0，在 时取得最大值 ，也不是很重要

之前也说了，

本身就是对

的近似，从下面动图也可以看出，越多的非平凡零点

参与运算（通过暴力计算得到），

越贴合

，近似效果比素数定理要好得多：

5.3 黎曼猜想

通过上面的分析，如果可以知道

函数的所有非平凡零点

，那么就可以得到精确的

。但是非平凡零点

求解的难度似乎不亚于得到素数精确分布的难度，怎么办？

如果知道

的范围也可以（下面

表示

的实部）：

• 如果 ：那么素数定理成立，这已经被证明了，历史上素数定理最初也是据此证明出来的
• 如果 ：这其实就是黎曼猜想的另外一种描述。如果黎曼猜想成立的，那就可以证出：
  也就是知道素数定理中的 到底与真正的 有多大的误差。

证明了黎曼猜想，我们就在素数分布上进了一大步。但这只是开始，离真正的素数分布还差得很远。

6 《素数之恋》

希望大家读完这篇文章可以对黎曼猜想有一个粗糙的了解，当然还有很多的疑问：

• 函数的非平凡零点 怎么就和素数的分布有关系？
• 函数是怎么扩张到复数域的？
• 为什么黎曼会猜想 ？
• 怎么就长那个样子？
• 定义成这样有什么动机？
• 关于非平凡零点 目前我们知道哪些？
• 

你可以把这篇文章看作一个大纲，或者《素数之恋》的读书笔记，所有的细节基本上都可以在这本书中找到。这本书也是我觉得写得最好的关于黎曼猜想的书。

7 写在后面的

黎曼这篇天才论文开辟了一个时代，其中很多结论虽然未经证明，但对于数学家这不啻于一座宝藏。

黎曼其人，出生贫寒，又遇上欧洲动荡、秩序重建，贵族自身难保，使得他很难像以往天才数学家一样可以获得贵族的资助。贫病交加之下黎曼 40 岁就因肺结核去世。仿佛天妒英才，上帝好像不想让人类过早地就拆穿了它所有的秘密。

如果黎曼活得长一些，说不定黎曼猜想就可以在他自己手中解决。不过不管怎样，素数的秘密，正如希尔伯特所说，“我们必须知道，我们必将知道”：

本文最新版本在（可能有不定期更新）：黎曼猜想到底说了什么？

更多内容推荐马同学图解数学系列